Astrolabe
From Inventions
| Line 5: | Line 5: | ||
|descrizione= | |descrizione= | ||
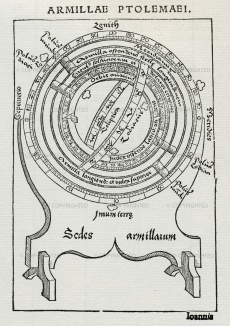
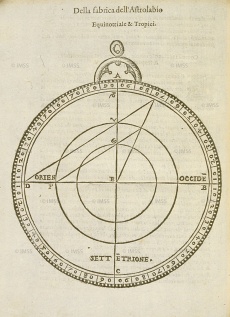
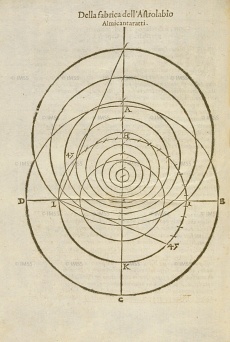
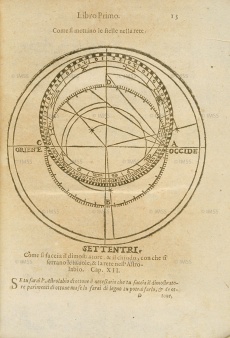
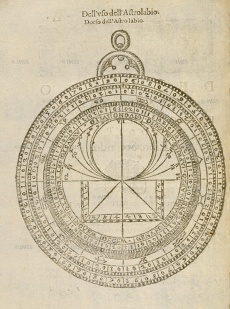
| - | Instrument perfected by Arab astronomers but already known, according to some scholars, to Apollonius and Archimedes (220 B.C.E.) and even to Eudoxus of Cnidos (350 B.C.E.). Better grounded is the belief that the astrolabe was known to Ptolemy (150 C.E.) and to Theon of Alexandria (375 C.E.), author of a treatise on the astrolabe that survived through the writings of the Syrian author Severus Sebokht, prior to 660 (O. Neugebauer, 1949). The instrument derives from a plane (stereometric) projection of Eudoxus’s armillary sphere, which represented the circles of the celestial sphere in three dimensions. These circles (the ecliptic and the tropics of Cancer and Capricorn) are projected onto the equatorial plane from a point situated at the South Pole, assumed to be the eye of an observer looking toward the northern hemisphere, according to the method described by Ptolemy in his ''Planisphere'' (ed. R. Sinisgalli, 1992). From this ideal viewing point the tropics and the equator appear as concentric circles centred around the North Pole, while the ecliptic appears off-centred and tangent to the circles of the tropics at the solstitial points. The horizon at the observer’s latitude is a circle passing through the equinoctial points (intersection of the ecliptic with the equator) and containing the circles of the ''azimuth'' (longitude) and ''almucantarats'' (latitude) converging toward the ''zenith'' (the point where a a vertical extending from the observer’s viewing point intersects the celestial sphere). Below the horizon, in the lower part of the instrument, are the lines of the seasonal hours (unequal) that pass through the twelve divisions traced on the arcs of circle of the Tropics and the equator comprised in this zone. The sixth hour is the only straight line, passing through the centre, which also represents the meridian. This diagram is usually engraved on a brass disk, on which rotates the so-called | + | Instrument perfected by Arab astronomers but already known, according to some scholars, to Apollonius and Archimedes (220 B.C.E.) and even to Eudoxus of Cnidos (350 B.C.E.). Better grounded is the belief that the astrolabe was known to Ptolemy (150 C.E.) and to Theon of Alexandria (375 C.E.), author of a treatise on the astrolabe that survived through the writings of the Syrian author Severus Sebokht, prior to 660 (O. Neugebauer, 1949). The instrument derives from a plane (stereometric) projection of Eudoxus’s armillary sphere, which represented the circles of the celestial sphere in three dimensions. These circles (the ecliptic and the tropics of Cancer and Capricorn) are projected onto the equatorial plane from a point situated at the South Pole, assumed to be the eye of an observer looking toward the northern hemisphere, according to the method described by Ptolemy in his ''Planisphere'' (ed. R. Sinisgalli, 1992). From this ideal viewing point the tropics and the equator appear as concentric circles centred around the North Pole, while the ecliptic appears off-centred and tangent to the circles of the tropics at the solstitial points. The horizon at the observer’s latitude is a circle passing through the equinoctial points (intersection of the ecliptic with the equator) and containing the circles of the ''azimuth'' (longitude) and ''almucantarats'' (latitude) converging toward the ''zenith'' (the point where a a vertical extending from the observer’s viewing point intersects the celestial sphere). Below the horizon, in the lower part of the instrument, are the lines of the seasonal hours (unequal) that pass through the twelve divisions traced on the arcs of circle of the Tropics and the equator comprised in this zone. The sixth hour is the only straight line, passing through the centre, which also represents the meridian. This diagram is usually engraved on a brass disk, on which rotates the so-called rete, a perforated disk representing the ecliptic, with the twelve signs of the zodiac, the tropic of Capricorn and the fixed stars of the eighth sphere. The whole is contained in a disk (''mater'') with raised edge (''limb'') engraved with the equal hour lines and the 360 degrees of the circle. This side of the instrument served to demonstrate the circumpolar motion of the stars and calculate their displacement, along with that of the Sun; to convert ecliptic into equinoctial coordinates and vice versa; and to read both diurnal and nocturnal time. On the other side of the astrolabe (''back'') a degree scale, zodiac and calendar are marked around the edge. In the lower part of the central disk is the shadow square used to measure distances and heights, both celestial and terrestrial. The shadow square, divided into twelve parts per side, reproduces the shadows cast by a vertical gnomon (''umbra recta'') or a horizontal one (''umbra versa''). Sighting is done through a diopter or alidade that shows the angle of inclination of the visual ray. As indicated by Juan de Rojas and Cosimo Bartoli, this side of the astrolabe also seems to have served for drawing in perspective: ''utilissimum proculdubio architectis, atque his, qui opticae rationem aliquid in pictura conatur delineare'' (Rojas, IV, XII); "which will be most useful to Architects, and to those who delight in using perspective in painting". (Bartoli, I, XXV). |
Revision as of 11:15, 27 July 2010
Used since ancient times, the name derives from the Greek astrolábon (from astron and lambánō, that which takes in/comprises the stars)
Contents |
Historic Period
2nd C. A.D.
Description
Instrument perfected by Arab astronomers but already known, according to some scholars, to Apollonius and Archimedes (220 B.C.E.) and even to Eudoxus of Cnidos (350 B.C.E.). Better grounded is the belief that the astrolabe was known to Ptolemy (150 C.E.) and to Theon of Alexandria (375 C.E.), author of a treatise on the astrolabe that survived through the writings of the Syrian author Severus Sebokht, prior to 660 (O. Neugebauer, 1949). The instrument derives from a plane (stereometric) projection of Eudoxus’s armillary sphere, which represented the circles of the celestial sphere in three dimensions. These circles (the ecliptic and the tropics of Cancer and Capricorn) are projected onto the equatorial plane from a point situated at the South Pole, assumed to be the eye of an observer looking toward the northern hemisphere, according to the method described by Ptolemy in his Planisphere (ed. R. Sinisgalli, 1992). From this ideal viewing point the tropics and the equator appear as concentric circles centred around the North Pole, while the ecliptic appears off-centred and tangent to the circles of the tropics at the solstitial points. The horizon at the observer’s latitude is a circle passing through the equinoctial points (intersection of the ecliptic with the equator) and containing the circles of the azimuth (longitude) and almucantarats (latitude) converging toward the zenith (the point where a a vertical extending from the observer’s viewing point intersects the celestial sphere). Below the horizon, in the lower part of the instrument, are the lines of the seasonal hours (unequal) that pass through the twelve divisions traced on the arcs of circle of the Tropics and the equator comprised in this zone. The sixth hour is the only straight line, passing through the centre, which also represents the meridian. This diagram is usually engraved on a brass disk, on which rotates the so-called rete, a perforated disk representing the ecliptic, with the twelve signs of the zodiac, the tropic of Capricorn and the fixed stars of the eighth sphere. The whole is contained in a disk (mater) with raised edge (limb) engraved with the equal hour lines and the 360 degrees of the circle. This side of the instrument served to demonstrate the circumpolar motion of the stars and calculate their displacement, along with that of the Sun; to convert ecliptic into equinoctial coordinates and vice versa; and to read both diurnal and nocturnal time. On the other side of the astrolabe (back) a degree scale, zodiac and calendar are marked around the edge. In the lower part of the central disk is the shadow square used to measure distances and heights, both celestial and terrestrial. The shadow square, divided into twelve parts per side, reproduces the shadows cast by a vertical gnomon (umbra recta) or a horizontal one (umbra versa). Sighting is done through a diopter or alidade that shows the angle of inclination of the visual ray. As indicated by Juan de Rojas and Cosimo Bartoli, this side of the astrolabe also seems to have served for drawing in perspective: utilissimum proculdubio architectis, atque his, qui opticae rationem aliquid in pictura conatur delineare (Rojas, IV, XII); "which will be most useful to Architects, and to those who delight in using perspective in painting". (Bartoli, I, XXV).
Bibliographical Resources
Bartoli, Cosimo. Del modo di misurare le distantie, le superficie, i corpi, le piante, le provincie, le prospettive, et tutte le altre cose terrene, che possono occorrere a gli huomini: secondo le vere regole d’ Euclide et degli altri più lodati scrittori. Venezia, F. Franceschi, 1564, I, XXV. Biblioteca Digitale
Chaucer, Geoffrey. A treatise on the astrolabe, in Gunther, Robert William Theodore. Chaucer and Messahalla on the astrolabe, in Early science in Oxford. Oxford, 1929.
Danti, Egnazio. Trattato dell'uso et della fabbrica dell'astrolabio. Con l'aggiunta del planisferio del Rojas. In Fiorenza, appresso i Giunti, 1569.
Danti Egnazio. Dell'uso et fabbrica dell'astrolabio et del planisferio di maestro Egnatio Danti. Novamente ristampato, et accresciuto in molti luoghi, coll'aggiunta dell'uso, e fabbrica di nove altri istromenti astronomici. Firenze, appresso i Giunti, 1578.
Gemma Frisius, Reinerus. De astrolabio catholico liber per Gemmam Frisium: quo latissime patentis instrumenti multiplex usus explicatur et quidquid uspiam rerum mathematicarum tradi possit continetur …. Antverpiae, apud Gregorium Bontium, 1556.
Messahalla. De compositione et utilitate Aastrolabii, in Gunther, Robert William Theodore. Chaucer and Messahalla on the astrolabe, in Early science in Oxford. Oxford, 1929.
Michel, Henri. Traité de l'astrolabe. Paris, Libr. A. Brieux, 1976.
Neugebauer, Otto. Studies in ancient astronomy: IX: The early history of the astrolabe, in «Isis», 40 (1949), pp. 240-56.
Neugebauer, Otto. A history of ancient mathematical astronomy. Berlin, Springer, 1975.
Neugebauer, Otto. Astronomy and history: selected essays. New York, Springer, 1983.
Reisch, Gregor. Margarita philosophica nova cui insunt sequentia. epigrammata in commentationem operis, institutio grammaticae latinae praecepta logices rhetoricae informatio ars memorandi ravennatis beroaldi modus compendi epi. arithmetica musica plana geometrie principia. astronomia cum quibusdam de astrologia philosophia naturalis moralis philosophia cum figuris. Stassburg, Grüninger, 1512.
Reisch, Gregor. Margarita filosofica del R.P.F. Gregorio Reisch: nella quale si trattano tutte le dottrine comprese nella ciclopedia. Accresciuta di molte belle dottrine da Oratio Fineo matematico regio, di novo tradotta in italiano da Gio. Paolo Gallucci. In Vinegia, presso Barezzo Barezz, 1599.
Rojas Sarmiento, Juan de. Commentariorum in astrolabium quod planisphaerium vocant: libri sex nunc primum in lucem editi : his additus est index capitum ac rerum quae toto opere continentur locupletssimus. Lutetiae, apud Vascosanum, 1550, IV, XII.
Saunders, Harold N. The atrolabe: a brief account of its history and construction together with practical instructions showing how it was used and can still be used for solving many astronomical problems. Bude, H.N. Saunders, 1971.
Saunders, Harold N. All the atrolabes. Oxford, Senecio, 1984.
Stöffler, Johannes. Elucidatio fabricae ususque astrolabii. Oppenheim, impressum Jacobum Köbel, 1513.
Tolomeo, Claudio. Il planisfero di Tolomeo. A cura di Rocco Sinisgalli, Salvatore Vistola. Firenze, Cadmo, 1992.
Turner, Anthony. Early scientific instruments: Europe 1400-1800. London, Sotheby, 1987.
Existing Instruments
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1113.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1112.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1105.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1109.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1107.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1110.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1106.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1108.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1096.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1114.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1111.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1282.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1123, 1124, 1127.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1095.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1093.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1100.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1098.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1097.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1103.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1094.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 3361.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1289.
Florence, Museo Galileo. Institute and Museum of the History of Science, inv. 1092, 660.
Images
Author of the entry: Filippo Camerota